PART I

INTRODUCTORY SUPPORTIVE EVIDENCES

Pauli’s Exclusion Principle and Quantum Numbers

The underlying cause of Pauli's exclusion principle has been the subject of much discussion.  Briefly, the principle states that no two electrons can have the same energy state characterized by the same four quantum numbers.  These numbers are represented by (n), the average distance from the nucleus; (l), space quantization of the orbital angular momentum; (m_s or s), space quantization of the electron spin; and (m_l), space quantization of the orbital momentum relative to the field.  What is the physical basis for these numbers?  They are the spatial coordinates of the electron within the positive and electric fields of the atom.

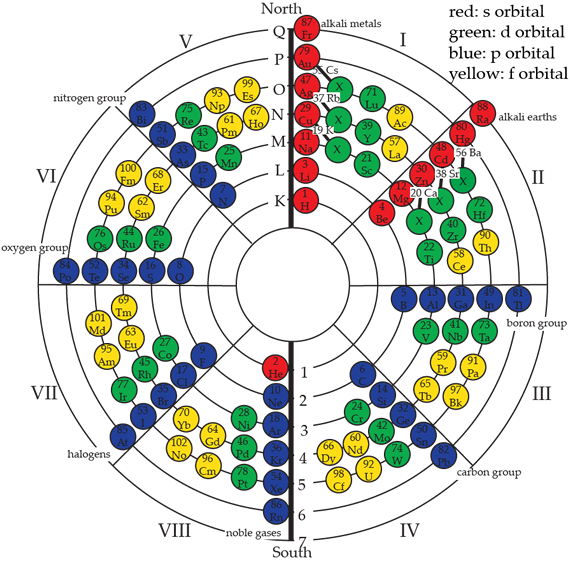
With the advent of quantum theory, a complete description of the electron within the atom became necessary.  Various motions of the electrons necessitated a numbering system and depended on the discipline letters or numbers which were used.  We also have old quantum numbers and new quantum numbers.  The spectroscopists used letters starting with K in their naming the major shells. The principle quantum number n equal to 1, 2, 3, 4, 5, 6, 7, is analogous to the spectroscopic shells K, L, M, N, O, P, Q. The term "principal" quantum number was used because 99 percent of the electron energy value in the description of the atom comes from this term.  In the Circular Model of the Atom the same relationship holds: the higher the shell or quantum number, the higher the energy of that particular atom. The following illustration shows the principal quantum number:

The azimuthal angular momentum number is denominated l, and, as its name implies, it is the rotational motion attributable to the circular spin in the atom.  The Circular Model uses the same nomenclature and values as does quantum theory.  Elements classify into azimuthal values of S (sharp), P (principal), D (diffuse), and F (fundamental) groups.

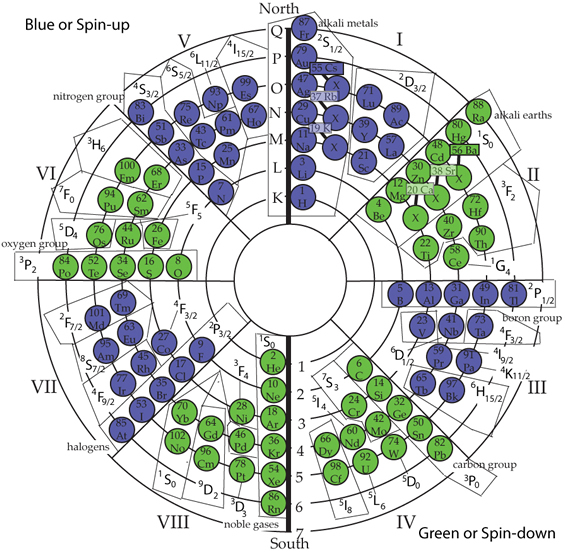
In the mid-1920s, while Wolfgang Pauli, Niels Bohr, and Werner Heisenberg were working on a quantum description of the atom, it was predicted that the description of the electrons in an atom should be defined by four degrees of freedom rather than the three degrees of freedom which was then being used.  Two young scientists, George Uhlenbeck and Samuel Goudschmidt studied the spectroscopic effects of line spectra and came to the conclusion that all electrons spin either +1/2, or -1/2, this resulted in a fourth degree of freedom in the description of the electron and the fourth quantum number. The Italian physicist, Ginestra Amaldi's, description of spinning electrons is concise.  "Uhlenbeck and Goudschmidt deduced that the spinning electron could adopt only two positions with respect to the field. In both cases the axis of spin would be aligned with the field's direction but in one case the spin of the electron would be clockwise, and in the other case anti-clockwise. That is, the spin could have only two values, plus one half and minus one half.  Thus if we put many electrons in a magnetic field-even a weak magnetic field-they would all become orientated with their axis parallel to the field but for some the axis would be in the same direction as the magnetic field and for others in the opposite directions"[1].  The Circular Model has all electrons naturally falling into a positive or negative field orientation, which then orients all odd integer electrons spin either a +1/2, or a -1/2, depending on the field.  This clears up many of the conflicts between the spectroscopic and theoretical physicists [2]. 

Previously, the magnetic moment has been described as a quantum rather than a classical electromagnetic phenomenon.  The current concept of the atom has the electrons orbiting in an electron cloud around the nucleus. However, it is also known that electrons have a characteristic spin, either +1/2 or -1/2.  If they are orbiting, they should show a transition phase from +1/2 spin, or -1/2 spin, or vice versa. This does not happen.  It seems to be an "either/or" situation, rather than a change, from one state to another. Not seeing a change we then must deduce that it is a field characteristic and that we have positive and negative portions of the field that are influencing the spins of the electrons up or down.  This is much more definitive in approach than a cloud having nebulous characteristics that defy description. The following Circular Model shows this relationship:

Quantum four magnetic moment description of an electron in the atom is the term m_l of which the value can be either -1, 0, or +1, etc. The Circular Model has within it the polarity attributes that fit the quantum magnetic moment numbers. For example: on one hand, if the element is a full integer ground state the electrons are balanced and will not be affected by the polarity of the field and will have a magnetic moment of 0. On the other hand, if the last unbalanced electron is in the positive field hemisphere portion of the Circular Model its magnetic moment value will be +1.  Conversely, if the last unbalanced electron is in the negative field portion of the circular table/model atom, its magnetic moment value will be -1.

[1] Amaldi, G., 1966. The Nature of Matter: Physical Theory from Thales to Fermi. Chicago: University of Chicago Press, pp. 82-83.

[2] Pauli's exclusion principle worked in establishing atomic electron configurations in the elements up to potassium, then irregularities set in because the (l) quantum number becomes more energy-important than (n). That is exactly the point where "electron sliders" fit into the Circular Model of the Atom.

previous

next