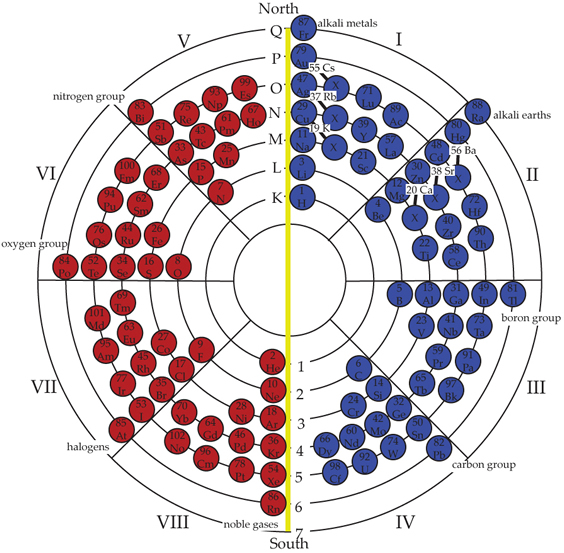
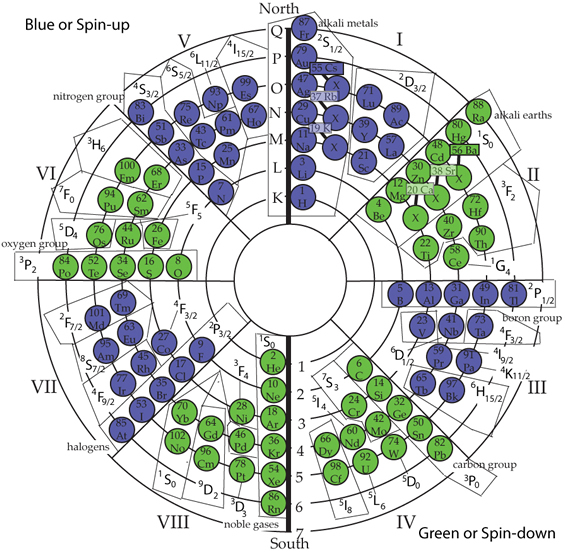
PART I

INTRODUCTORY SUPPORTIVE EVIDENCES

Magnetism and Monopoles

In Einstein's early years, one of his favorite play things was a magnet which was given to him; he told of the great interest that developed in his formative years towards magnetism and electricity. How often has a magnet been broken in half and the two pieces became smaller magnets each with similar north and south polarity?  What characteristic of the elements could possibly produce this positive and negative field unless the field was within the structure of each atom?  The Circular Model with its positive and negative polarity field approach provides the answer as to why the broken magnet pieces still retain the positive and negative polarity.      

Every atom has this characteristic.  It is what causes quantum gases to be diamagnetic and other elements to show trace splitting in a Stern-Gerlach type experiment. Quantum description of gases has a diamagnetism which the old classical atomic theory could not explain.  The Circular Model indicates that every element, gas or otherwise has an opposites factor that shows up as a subtle diamagnetism within its electron-atom structure. A hypothesis should be considered wherein the classical atom approach based upon the Circular Model has the values, diamagnetism, electron spin, etc., which quantum theory states is not visualizeable.

One of the major questions in physics today is whether there are such things as magnetic monopoles.  Positive or negative monopoles have never been found. In fact it has been questioned by some whether they can exist independently.  Some physicists believe monopoles are comparable to a free electron having its own field.  This contrasts with the author's hypothesis that magnetism is a result of the ordering system of the electron and nucleon buildup with alternating full integer and half integer spin fields as the atom builds up. Magnetism is a function of the geometric structure of atomic matter being in positive and negative fields.

Law of alternation of multiplicities of 1/2 integer spin fermions combining to form full integer octets resulting in family groups with similar spin states within each family.

Is there a massive monopole for each atom's positive and negative tendencies?  Examining an electromagnetic wave it is observed to have a positive vector component and a negative vector component, each diametrically opposite in purpose, but still one wave. An electromagnetic wave is considered to be singular, but both vector components are of opposite sign. Again, in the example of the electromagnetic wave, we have opposites joining together to create a wave entity. Likewise, opposite sign matter, joins together to form a neutral atom. In the case of the electromagnetic wave, is it necessary to have monopoles both positive and negative at each point of the wave to transmit electromagnetic energy?  No, opposite components are necessary both in waves and atoms.  Monopoles are governed by the same law of duality and do not occur as separate entities.

previous

next