The Circular Model of the Atom

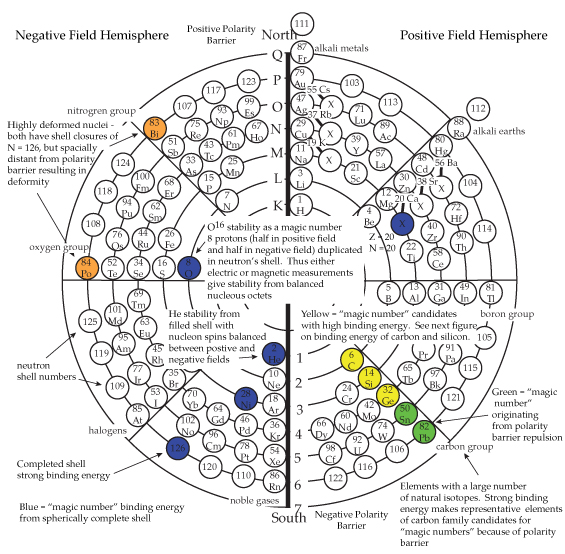
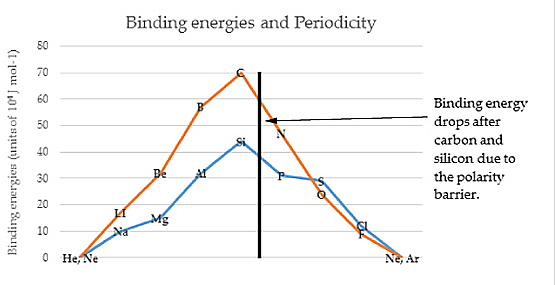
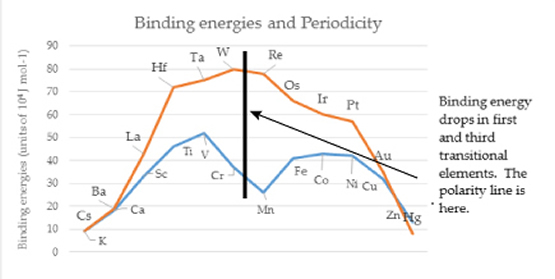
PART I

INTRODUCTORY SUPPORTIVE EVIDENCES

Nuclear Shells and the Collective Model

Maria Meyer's work on nuclear shell theory resulted in a model with specific nucleons as strong points. The next added nucleon manifesting lower binding energy established what she considered to be closures of nuclear shells. Substantial nuclear binding energy-drops occur in the next element of the periodic table after group IV (carbon family) elements. In the Circular Model the binding energy drops where the flip occurs at the polarity barrier. This suggests a structure that is more than randomly statistical in nature, evidencing similarities between the nuclear and atomic shells.

Herzberg stated. “These hyperfine structures can be quantitatively explained, however, when it is assumed (as for the electron) that the atomic nucleus possesses an intrinsic angular momentum with which is associated a magnetic moment” [1]. The magnetic moment referred to, can be a key, along with Pauli's exclusion principle, and the Circular Model of the Atom to nucleon placement and stability.

The magic numbers of proton and neutron combinations in the nucleus are due to atomic structure. Some new number combinations have suggested nucleon stability at elements and isotopes not considered in the past. The advent of the new numbers, raises the question whether all of the magic numbers stability is caused by the same conditions? Are the geometrical shell closures the predominant cause of the stability? The present magic number list is 2, 8, 20, 28, 50, 82, and 126. Generally, it is thought that nuclei that match have one closed shell, either proton or neutron.

An analysis of the Circular Model with its dipole approach, suggests that magic numbers, with one exception (oxygen), originate in pushing the next nucleon through a polarity barrier (for example tin ₅₀ and lead ₈₂), or shell closures (for example calcium ₂₀ and nickel ₂₈) in connection with "sliders" of the Circular Model. Oxygen, with eight protons and eight neutrons, fits within the field positive and negative octet configuration. Each oxygen nucleon fits into an octet position by having one proton and one neutron in both positive and negative states. Thus giving stability to the nucleons in either electrical or magnetic force situations. This is why O₁₇ is such a spontaneous beta emitter, no stability positions for it to fill in.

The case can be made that all the representative elements along the fourth octet ray, (carbon, silicon, germanium, tin and lead) should be considere magic numbers in the context of binding energy. Also it has been suggested that element number 14, (silicon), should be considered [2].

Why should binding energy drop when moving from the carbon group to the nitrogen group elements in the periodic table? This is the point where inverted multiplets occur and vectors change from their original orientation. Why? Because there is a polarity barrier within the atom, and once over the barrier, then a resultant binding energy changes from the positive to negative field.

Source: Puddephatt, R. J. and Monaghan, P.K. 1986. The Periodic Table of the Elements. Oxford Chemistry Series 32, Second Edition. Clarendon Press, p. 33.

Source: Puddephatt, R. J. and Monaghan, P.K. 1986. The Periodic Table of the Elements. Oxford Chemistry Series 32, Second Edition. Clarendon Press, p. 72.

J. H. Hamilton and J. A. Maruhn working with exotic nuclei found half-filled shell stability. “Conversely, among deformed nuclei the ‘hardest ones,’ namely the ones with the greatest stability in their properties, are the ones that are farthest from any spherical magic number: their shells are half filled in regard to both neutrons and protons” [3]. Why should half-filled shells provide stability? We usually think of filled shells as providing this function. The case can be made that the stability of half-filled shells is caused at that point by resistance in moving the fermions into a positive or negative field different from its present location.

If we look at elements with neutrons of magic numbers from the basis of the Circular Model, then we see the stability comes from "sliders" filling a complete shell in a manner not considered before, and secondly, from the polarity barrier hypothesis of half-filled shell flips of the Circular Model of the Atom.

While the nuclear shell model meets the issue of "magic numbers" and energy levels, it doesn't address the deformed core issue. Closed shells are usually regarded as symmetric, but a large quadropole moment denotes a deformed nucleus. Deformations suggested by quadropole radiation were much greater than could be accounted for by the shell model. A "liquid drop" model was developed, that addressed the quadropole problem, but eventually a "collective model" incorporating aspects of both was developed. But, the basic problem hasn't been solved, namely two nuclear theories incapable of integration into a rational single theory. The Circular Model of the Atom with distinct positive and negative fields is the basis of the deformed core. When the "Lanthanide Contraction" is combined with the Circular Model, it gives distinct evidence that increased negativity in a system has a contracting effect on that system. In the nuclear core case the deformation from spherical is in the range of 7% [4]. The range of this inequality evinces the subtle aspects of broken symmetry in the nuclear strong force. Non-stoichiometric compounds formation is evidence of broken symmetry at the electromagnetic level. The gravitational force range suggests broken symmetry is universal. Features of half-filled shell characteristics subtly crop up through in all physical processes.

Another way of looking at the half shell stability phenomena is Pauli's 180 degree spin matrices changing sign by pushing the next electron across a polarity line. The polarity line of the circular periodic table/model of the atom is more than just a nice symmetry. T. E. Jordan, in his book on quantum mechanics observed magnetic effects. “Magnetic fields exert forces on objects that have magnetic moments..., They appear to be the same for atomic particles for macroscopic objects” [5]. This half-shell stability suggests steadiness along its longitudinal axis caused by the balancing of internal fields. Eisberg and Resnick noted binding energy build-up at magic numbers: “about 2 MeV of extra binding energy is found at each magic number” [6]. Why do we have a buildup of binding energy unless we have an obstruction? What is the barrier? The polarity wall between the positive and negative fields has to be overcome.

Hamilton and Maruhn also pointed out in their Scientific American article that: “The excited states represent successively more energetic rotations resembling those of a football tumbling end over end. (In quantum mechanics, a prolate or football-shaped nucleus can tumble end over end, but cannot spin about its long axis.) It is as if a football could be place-kicked but could not be given a spiraling forward pass” [7]. Why do nucleons not exhibit normal rotations? The atomic and nuclear polarity line prevents the nucleons from moving from one orientation to another. They can cartwheel, but not roll within the atom.

In the same article, the authors point out that certain exotic isotopes of mercury show dual “personalities.” The element mercury is in octet II of the Circular Model and thus conforms with the 'slider' hypothesis of possible events in octet I and II of the model. Slight changes in electrical and magnetic values can be the cause of a number of different spectral effects. Pauli recognized this area of the atom as the cause of the anomalous Zeeman effect. “All the basic 'matter-like' particles - electron, protons and neutrons - obey the Pauli principle”[8]. If the fermions in the nucleus obey Pauli's Exclusion Principle and we follow the building up principle, then the nuclear magnetic moment and the atomic transition electron from emission electron to absorption electron would be along the same plane. This non intermixing of fermions later showed up in the non-commutative formulas of quantum mechanics.

This separation of protons into two non-mixing positive and negative fields perhaps was alluded to in Lee and Yang's famous paper on non-conservation of parity. “As is well known, its violation implies the existence of a right-left asymmetry.... These experiments test whether the present elementary particles exhibit asymmetrical behavior with respect to the right and left. If such asymmetry is indeed found, the question could still be raised whether there could not exist corresponding elementary particles exhibiting opposite right-left symmetry. If this is the case, it should be pointed out that there must exist two kinds of protons, P(r), and P(l): the right-handed one and the left-handed one” [9]. This is the nuclear state of the atom based on the Circular Model that is supported by the parity violations of Lee and Yang.

Dirac in his Nobel lecture suggested that positive and negative protons may exist. “One might perhaps think that the same theory could be applied to protons. This would require the possibility of existence of negatively charged protons forming a mirror-image of the usual positive charged ones...if this symmetry is really fundamental in nature, it must be possible to reverse the charge on any kind of particle" [10]. This has in fact been done, but the same argument can be made for having them incorporated within a model of the atom. By doing so it explains the broken symmetry of the weak force radioactive decay.

Interestingly, the by-products from an atomic fission reaction generally result in the largest fragments being lead or tin isotopes. This suggests stability along either side of the point of inversion following octet IV of the representative elements. This is one of the two octets next to the polarity line and an area of natural binding energy drop. It is suggested that there is a relationship between the nucleons drop in binding energy and the ‘flip’ characteristics of the electrons as evidenced by the Circular Model of the Atom. Quantum theory's statistical approach does not allow for sub-atomic particles to have the specific position and individuality as provided by the Circular Model.

[1] Herzberg, G., 1944. Atomic Spectra and Atomic Structure. New York: Prentice-Hall, p. 185.

[2] Nix, J. R., 1987. Private conversation [interview] (10 December 1987).

[3] Hamilton, J. H. & Maruhn, J. A., 1986. Exotic Atomic Nuclei. Scientific American,July, 255(1), p. 82.

[4] Frauenfelder, H. & Henley, E. M., 1991. Subatomic Physics. Englewood Cliffs(New Jersey): Prentice-Hall, p. 514.

[5] Jordan, T. E., 1986. Quantum Mechanics in Simple Matrix Form. New York: John Wiley & Sons, p. 61.

[6] Eisberg, R. & Resnick, R., 1985. Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles. 2nd ed. New York: John Wiley& Sons, pp. 556-557.

[7] Hamilton, J. H. & Maruhn, J. A., Exotic Atomic Nuclei. Scientific American. July, 255(1), pp. 83-84.

[8] Hey, T. & Walters, P. 1987. The Quantum Universe. Cambridge: Cambridge University Press, p. 115.

[9] Lee, T. D. & Yang, C. N., 1956. Question of Parity Conservation in Weak Interactions. Physical Review, 104(1), p. 258.

[10] Dirac, P. A. M., 1933. Nobel Prize in Physics Award Address. Elsevier Publishing Co.