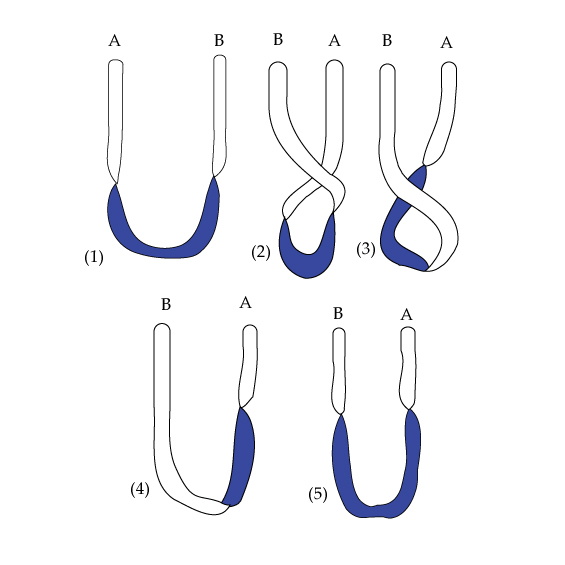
PART I

INTRODUCTORY SUPPORTIVE EVIDENCES

Unique Electron Flip

A unique characteristic of the Circular Model is the polarity 'flip' of the electrons as they build-up to make the elements.  Electrons in atoms, build-up until they get half way through each shell, then flip into the negative field to build up the opposite half shell. The description of spin, as provided by Uhlenbeck and Goudschmidt, is that electrons can spin either +1/2 or -1/2, no variation is found.  This is a result of the electron being either in a positive or negative field. There is not a neutral field within the atom.

Electrons have the quantum characteristic requiring 720 degrees to describe rotational path characteristics within the atom. Use of the Circular Model can provide a classical explanation for this phenomenon.  Starting at some arbitrary point, for example 12:00, an electron would go to 6:00, which would be 180 degrees from the start, then flip to the left side of 12:00, which would be 180 degrees from the 6:00 position down the negative field to left of 6:00, then flip back to the beginning position.  This results in the 720 degree path of an electron in any atom.

Dirac, and Feynman later, used the illustration of the ends of a belt being twisted 360 degrees switches the ends of the belt. A further 360 degrees restores it completely to the original state. We have the same situation in tracking electron buildup in the atom and intrinsic spin of the electron.

Feynman's 720o Belt Example

In the sequence (1) to (3) the ends of the belt have been reversed in positon. Note that the twist on the right-hand side in (5) comes out opposite that in (1). To restore it completely, an additional 360o turn of the right belt around the vertical would be necessary. From: Feynman, R. P., 1987. Elementary Particles and the Laws of Physics: The 1986 Dirac Memorial Lectures. Cambridge University Press: Cambridge.

One of the inexplicable attributes of the quantum electron derived from Dirac's equation is a peculiar type motion, known as intrinsic spin.  This is a form of angular momentum that, when rotated through its axis, does not return to its original state in a 360 degree rotation but needs a 720 degree path to arrive back at its origin.  Related to this double value of spin is the magnetic field giving values twice the amount that a rigid ball spinning would give.  The flip concept, illustrated by the electrons in Circular Model of the Atom demonstrates that the spinning ball concept of 360 degrees rotation is not sufficient.  An inversion process of 180 degrees is necessary in moving electrons from one field to another, then an additional 180 degrees to return to the original position. A complete description of electrons within the atom requires 720 degrees. Evidence to the effect that the electron path go through a `flip' process in atomic buildup halfway through each shell is provided by inverted spectra that occur when shells become half filled. Bohr also attempted to find shell closures halfway through each shell.        

The distinctive flip of the Circular Model of the Atom has a deeper reason for its existence than just organizational placement of electrons.  We know for example that the electromagnetic wave has two components, the electric wave portion with vectors pointing in one direction as it propagates in space, and the magnetic wave portion perpendicular to the electric wave component, but with inverted vectors.   Prince Louis de Broglie expanded on the wave-particle duality in that radiation waves are equally applicable to matter. Yet we are not carrying the dual nature of energy waves into the atomic structure. Evidence of this duality results in half-filled shells and opposite energy fields. 

G. K. Woodgate's book on atomic structure mentions half shell problems.  "Because of this symmetry about the half-filled shell it follows that the fine structure vanishes, in first order, for all terms of a half-filled shell in LS coupling.... One finds in the tables of energy levels that experimental fine-structure splittings are listed for half-filled shell configurations, but these are small and are usually due to breakdown of the coupling scheme.... There are, however, anomalies in the magnitude of the fine-splitting in the alkalis which we shall not discuss" [1]. According to Eisberg and Resnick, the fine-splitting problem included hydrogen. "A simple example is the Zeeman effect for hydrogen atoms.  In their ground state these atoms have no orbital angular momentum, and therefore no orbital dipole moments.  But the measurements show that their ground state energy level is split by the applied magnetic field into two components, symmetrically disposed about the energy of the ground state in the absence of a field. This splitting reflects the two possible values of the orientational potential energy"[2]. This double value within the atom eventually shows up in the more complex atoms as significant half-filled shells and inverted multiplets.

These half-filled shells are vital to the understanding of the atom as to inverted multiplets, emission and absorption spectra, negative mass, and other atomic phenomena, was noted by Herzberg citing Hund: "Multiplets formed from equivalent electrons are regular when less than half the shell is occupied, but inverted when more than half the shell is occupied" [3]. Eisberg and Resnick further noted; "If the optically active electrons are in a more than half-filled subshell the sign of the spin-orbit interaction is reversed because the atom acts as if it had positively charged holes instead of negatively charged electrons, which reverses the relative orientation of the magnetic dipole moment and angular momentum vectors"[4]. Dirac, in his Nobel lecture noted, "...since we find from the theory that if we disturb the electron, we may cause a transition from, a positive-energy state of motion to a negative energy one" [5]. This is what happens to the bound fermions within an atom resulting in what we call the "flip" of part of the fermions making up each atom when the building-up principle creates a positive and negative field as evidenced by inner core +1/2 or -1/2 spin states.

Taking the binary hydrogen compounds, LiH, BeH², B₂H₆, CH₄, NH₃, H₂O, and HF, then in the above sequence of compounds, H. Sisler in his book on electron structure and periodicity noted that, "the polarity of the M-H bond (a specific element-hydrogen) changes direction.  In lithium hydride the charge on the hydrogen atom is negative, whereas in the highly polar hydrogen fluoride molecule, the hydrogen atom forms the positive end of the dipole. The physical and chemical properties of the compounds reflect this change in polarity" [6].  These are all compounds of hydrogen on the "K" shell, with the elements of the "L" shell excluding neon.  Where does the change in polarity occur?  If we tie this together with Hund's half-filled shell rules, then it should occur between carbon and nitrogen.  This is the point where the positive or negative electron spin orientation is weakest from the respective field polarity strength position.

Further evidence of a half-shell polarity change can be suggested from semiconductor physics.  We can have two types of conductivity when we dope Silicon or Germanium. If we dope from Group III elements we get P-type (defect) semiconductors. Moving to the other side of the Group IV elements, (silicon and germanium), and doping with Group VI elements we get n-type (excess) semiconductors. One acts as an electron acceptor and one acts as an electron donor. This suggests a polarity barrier as evidenced by the Circular Model of the Atom.

How do the electrons orient themselves within each respective field? There is a system of standing waves, at which each wave node is an electron.  Perhaps, if we think in terms of a sea wave, it can be visualized.  A. d'Abro's description is appropriate: "Thus, if a train of plane waves is advancing over the surface of the sea and is reflected by a wall, the incident and the reflected trains interfere.... Along intermediary lines (nodal lines) the water remains still" [7]. These nodal points form the system of atomic rays upon which Faraday built his theory of electrical and magnetic fields, which Maxwell later formalized. Think of the positive and negative polarity line of the Circular Model of the Atom as a wall that is a reflective point necessary for establishing the standing waves that make up the atomic shells.  We get inverted (negative spin orientation) electrons and nucleons in the negative field that form absorption spectra.

Within the atom, it is necessary to have a structure to accommodate the dissimilarities of the total electromagnetic wave.  The reason that dissimilar emission and absorption spectra emit waves from the discrete atom is that both are accommodating totally dissimilar components of the electromagnetic wave interacting with matter.  If the concept of the Circular Model is followed, then dissimilar components are necessary for atomic existence.  This is why we get discreteness.  The current concept of an electron cloud is incorrect, because that model doesn't account for electron spin within the cloud.  Yet the spectroscopic analysis of the elements shows a certitude that an electron cloud does not provide.

A description of a changing field is provided by H. Skilling: "A changing magnetic field induces an electric field, both in the region in which the magnetic field is changing and also in the surrounding region; likewise a changing electric field produces a magnetic field in the region in which the change takes place and also in the surrounding region.  Consequently, when there is a disturbance of either the electric or magnetic conditions in a given region of space, the disturbance cannot be confined to that space.  The changing fields within that region will induce fields in the surrounding region also, and those, in turn, in the next surrounding space, and energy is propagated outward.  As this action continues a wave of electromagnetic energy is transmitted" [8].

Continuing with the transmission of electromagnetic waves, the Circular Model provides the ray components necessary for the radiation of light. This conforms with Eisberg's and Lerner's description of light. "Light appears to travel along rays (in other words, along well-defined paths like billiard balls) obeying the laws of ray optics...)" [9].  The quantum atom is not structured toward a ray approach explanation.

What, then, is an electromagnetic wave?  Using the example of a coaxial cable, with voltage and waves moving along it, the electric field (E) is radial and perpendicular to the cable axis, and the magnetic (B) field is circumferential.  At every point E and B are at right angles to each other, the same can be shown for "free" waves without the benefit of the cable.

Wave equation solutions usually have two parts, for example, an electric field portion and a magnetic field portion. This duality was noted by Skilling, "The first part of this solution...represents a wave traveling in the direction of the X axis. ...The second part of the solution is also a traveling wave, but it represents a wave traveling in the negative X direction.  Thus the complete solution describes two traveling waves, one going in each direction, simultaneously passing through the same space, and the equation informs us that they travel independently of each other"[10].

Here, with electromagnetic waves, as well as the Circular Model of matter, we have totally dissimilar components making up an entity. It is the very core of reality.

[1] Woodgate, G. K., 1980. Elementary Atomic Structure. 2nd ed. Oxford: Oxford University Press, pp. 131-133.

[2] Eisberg, R. & Resnick, R., 1985. Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles. 2nd ed. New York: John Wiley & Sons, p. 274.

[3] Herzberg, G., 1944. Atomic Spectra & Atomic Structure. New York: Prentice-Hall, p. 135, italics in original.

[4] Eisberg, R. & Resnick, R., 1985. Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles. 2nd ed. New York: John Wiley & Sons, pp. 370-371.

[5] Dirac, P. A. M., 1933. Nobel Prize in Physics Award Address. Elesevier Press.

[6] Sisler, H. A., 1963. Electronic Structure, Properties, and the Periodic Law. New York: Reinhold Publishing Corporation, p. 104.

[7] D'Abro, A., 1951. The New Physics. New York: Dover, p. 271.

[8] Skilling, H. H., 1948. Fundamentals of Electric Waves. New York: John Wiley & Sons, pp. 112-113.

[9] Eisberg, R. & Lerner, L., 1981. Physics Foundations and Applications. New York: McGraw Hill, p. 1434.

[10] Skilling, H. H., 1948. Fundamentals of Electric Waves. New York: John Wiley & Sons, pp. 120-121.

previous

next