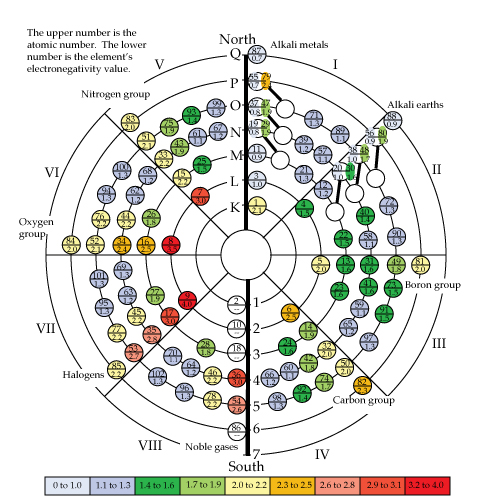
PART IINTRODUCTORY SUPPORTIVE EVIDENCESElectronegativityAn approach to the measurement of electron bonding between different elements was established by Pauling. He measured the strength of the electron bond between elements and established an electronegativity scale for the elements. “An additive constant has been so chosen as to give the first row elements carbon to fluorine the values 2.5 to 4” [1]. In the L shell starting with lithium and ending with fluorine, each element gains .5 in higher electronegativity. In the M shell starting with sodium and ending with chlorine, the values gain .3 to .4 with each succeeding electron, excluding the inert gases. By extending these values to the various elements within the same shell,(for example lithium has a value of 1), and extending the values outward and radially within families, we get a development of a ray approach that is a visual characteristic of the Circular Model.
The radial arms of the various octets of the Circular Model show descending values from the inner shells to the outer shells within the same family. For example, the Halogen family in group VII: fluorine at 4.0, chlorine at 3.0, bromine at 2.8, iodine at 2.7, and astatine 2.2, illustrates the descending values within that family. By placing the electronegativity values within the concept of a field with positive and negative polarity, it suggests a build-up of the elements and electrons that is controlled by an inherent polarity within each element. The total configuration of the electrons produces a neutral atom. Another symmetry of the Circular Model is that in each series family, (ex. halogen's, alkali metals etc.) all of the ground state spin is the same, and its opposite counterpart one hundred eighty degrees away has opposite spin. For example, the alkali metal group all have spin +1/2, and is opposite the inert gases that all have full integer spin. This raises the question of whether Boson-Fermion statistics apply to all the individual full integer spin elements of the periodic table. A recent book on quantum physics raises the question in regard to helium. “As we have said, matter-like particles, such as electrons, protons and neutrons are all fermions, so why should helium be considered a boson? The reason is that the usual 4He atom contains an even number of fermions: two protons and two neutrons in the nucleus, and two atomic electrons. Experiment tells us that elements with an even number of fermions can behave like bosons” [2]. Is the only difference between fermions and bosons the non-paired positive or negative spin that fermions have? [1] Pauling, L., 1960. The Nature of the Chemical Bond. 3rd ed. Ithaca, New York: Cornell University Press, p. 89. [2] Hey, T. & Walters, P., 1987. The Quantum Universe Cambridge: Cambridge University Press, p. 116. |
 |
- Home
- The Circular Model
- Quantum Charts
- Model Physics
- Part I: supporting evidences
- introduction
- Pauli's exclusion principle
- dipole magnet
- unique electron flip
- polarity and anomalous angular momentum
- lanthanide contraction
- Stern-Gerlach
- electron tunneling
- discreteness
- electronegativity
- Compton effect
- Dirac's equation
- symmetry
- gyromagnetic ratio
- nulcear shells
- Kaluza-Klein
- gravity
- magnetism and monopoles
- Heisenburg uncertainty principle
- missing mass
- Olbers' paradox
- Big Bang
- Part II: spectral evidences
- Part III: fine structure constant
- Part IV: superconductivity
- Part V: sub-atomic particle physics
- Part VI: summary
- Part I: supporting evidences
- Astrophysics
The Circular Model of the Atom is a circular periodic table that shows atomic structure in addition to periodicity. Unlike any other periodic table or model, it demonstrates that the atomic structure has an inherent dipole magnet that create positve and negative fields and elemental qualities at the atomic level.
The Circular Model of the Atom was created by Helen A. Pawlowski in the 1980s, and published in her work, Visualization of the Atom. Her brother, Paul A. Williams extended many of Helen's ideas with his examination of the standard model using Helen's Circular Atom Model. This website contains some of Helen's ideas and Paul's writings.
Binding energy drops off between carbon and nitrogen and silicon and potassium is explained.
The model correctly accounts for the Madelung-rule (or Goudsmit rule).
The model provides an explanation for the lanthanide contraction.
1. Atoms are dipole magnets at the atomic level.
2. Demonstrates Hund's half filled shells, electron tunneling, and a visulalizable aufbau buildup of the elements.
3. Visual explanation of Anomalous Zeeman Effect.
4. Strong and weak patterns revealed.
5. Lanthanide contraction is explained.
6. Provides a visual basis for ferromagenetism, paramagnetism and antiferromagnetism.